padding oracle attack 原理

2024-06-07

Uncategorized

4.6k words

首先需要理解的是异或，这个非常简单，举几个例子


0 ^ 1 = 1

1 ^ 0 = 1

0 ^ 0 = 0

1 ^ 1 = 0

一个数值 ^ 另一个数值 = 亦或中间值

一个数值 ^ 亦或中间值 = 另一个数值

另一个数值 ^ 亦或中间值 = 一个数值

任意数值 ^ 0 = 任意数值

接下来是一个利用思路，如果我们此时有一个字符串是10086,我们将其与一个iv进行简单的亦或.

10086 变化成下面这个亚子

0x31 0x30 0x30 0x38 0x36

iv = 0x6b 0x72 0x62 0x76 0x67

然后进行对应的亦或,变成

0x5a 0x42 0x52 0x4e 0x51

此时如果想让他变回"10086"只需要再和iv亦或一次即可。

但如果我要将其"10086"在亦或后变成其他数值的话，只需要操作iv即可。

比如我要把"10086"与iv亦或后变成20086。

我就可以将"1"与iv亦或后的0x5a，与"2"的hex进行亦或，比如这样

1
2
3

"2" = 0x32

0x5a ^ 0x32 = 0x68

由

1
2
3

一个数值 ^ 另一个数值 = 亦或中间值

一个数值 ^ 亦或中间值 = 另一个数值

此时0x68就是我们第一次iv后的0x5a 与 "2"的 0x32产生的中间值

所以我们只需要替换掉iv的0x5a变为0x68即可实现在iv亦或时将0x5a变更为2

如下

a=['0x5a', '0x42', '0x52', '0x4e', '0x51']

b=['0x68', '0x72', '0x62', '0x76', '0x67']
 for i in range(len(a)):
     print(chr(int(a[i],16) ^ int(b[i],16)),end="")
 
20086

这样就通过替换iv变为，要变换的目标值和cipertext的亦或中间值即可实现解密后的数值变更为我们要变换的目标值。

Padding Oracle Attack 这里采用和这位师傅相同的的8字节padding做演示，这个padding也是这个攻击实现的核心原因。

这里了解一下补位

https://zhuanlan.zhihu.com/p/672527050

因为是8字节的，所以如果字节数不满8字节的情况下需要补位

cip1

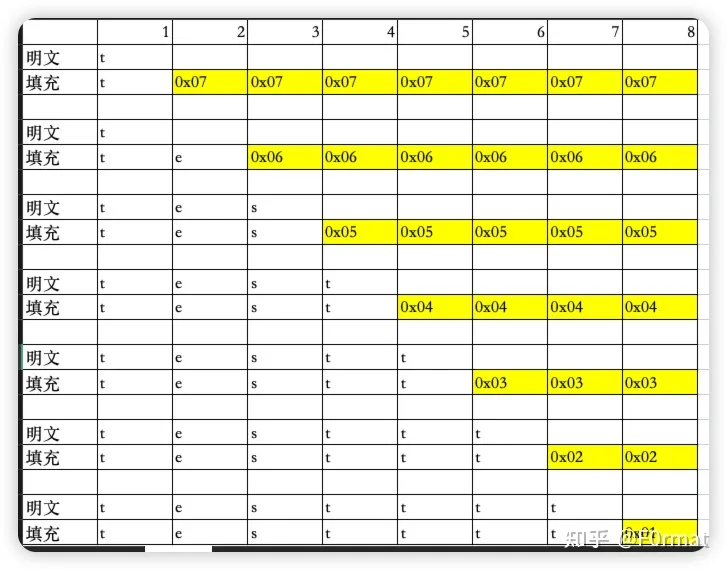
比如我们明文是

0x62,0x61,0x62,0x61,0x62,0x61,0x62

加密时候因为不足8位，有了7位所以最后需要补一个0x01，明文就变成了

0x62,0x61,0x62,0x61,0x62,0x61,0x62,0x01

这就是补位了，如果你缺俩那就补俩0x02，如果你缺仨那就补三个0x03，如果缺10个建议直接补钙

上面的都沾点废话了，就是基础的补位，下面才是正经的部分

这里是padding oracle attack

这个部分参考

https://buaq.net/go-35066.html

这里借鉴了文中这位师傅的说法

Ciphertext经过block cipher decryption后的值称为Inermediary Value也就是iv

侬可能会好奇block cipher decryption是啥，因为cbc模式的是先过一边iv，然后再过一遍奇妙的加密，才有的密文。

解密也是先过一遍奇妙的加密，再过iv。（困得慌不想细写这个玩意，因为和这个攻击实现其实没啥关系..主要是系统那侧加解密的，我们需要关注的只有iv）

因为cbc是由上一个密文作为iv对下一个进行异或加密嘛，所以可以控制密文1来对密文2来获取中间值也就是上面师傅说的Inermediary Value，具体怎么获得中间值这个就是padding oracle attack存在的意义。

需要注意padding oracle attack实现的前提之一是需要能发起产生交互服务端，并且能对padding补位是否成功的情况做出反馈.

假如我们有两个16字节的Ciphertext 方便看所以下面对应了他的明文Plaintext

Ciphertext

1[0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00]

2[0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00]

Plaintext

1[0x7c 0x42 0xda 0x7b 0x84 0xa2 0x77 0xb1 0x31 0x37 0x1f 0xcd 0xbe 0x3e 0x23 0x1c]

2[0x4a 0xec 0xf6 0xed 0x58 0xfc 0xdc 0xa4 0xa3 0x4a 0x39 0x25 0x39 0x5b 0xeb 0x42]

我们直接给ciphertext全0，然后可以通过给Ciphertext 1的最后一位轮询出一个值，来使得的Plaintext 2最后一位符合0x01，也就是符合padding规则，说白了padding规则只看你明文符不符合规矩就是了

这里按照上文中师傅给出的

Ciphertext

1[0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x43]<-当这里给了个0x43的时候下面明文2变成0x01了

2[0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00]

Plaintext

1[0x3d 0x10 0xc6 0xbc 0x68 0xe7 0xdd 0xc4 0xc1 0x75 0x65 0x85 0x6a 0x3d 0xef 0x92]

2[0x4a 0xec 0xf6 0xed 0x58 0xfc 0xdc 0xa4 0xa3 0x4a 0x39 0x25 0x39 0x5b 0xeb 0x01]<-这里异或后便乘0x01啦符合padding规则了，服务端就会不报错了

其实这个时候虽然服务器侧不报错了，但如果我们在不知道明文的情况下，如果不确定可以再给密文1倒数第二个随便一个值避免瞎猫撞死耗子，比如这样

Ciphertext

1[0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x08 0x43]

2[0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00]

Plaintext

1[0x3d 0x10 0xc6 0xbc 0x68 0xe7 0xdd 0xc4 0xc1 0x75 0x65 0x85 0x6a 0x3d 0xef 0x92]

2[0x4a 0xec 0xf6 0xed 0x58 0xfc 0xdc 0xa4 0xa3 0x4a 0x39 0x25 0x39 0x5b 0xe3 0x01]

可以看到还是符合的,只要不是乱给明文倒数第二个变成0x01就不会报错..因为如果要出现俩补位的就是要填充0x02了，所以俩0x1会报错，这里是为了确定我们操作密文1影响到明文2出的倒数第一位明文是0x01，而不是出现了类似俩0x2或者别的也能通过padding情况，所以要再倒数第二位也再试一下捏，我们要保证的就是这一轮先确保padding的是0x1，等下一位才能用到0x2padding.

这里假使在我们不知道明文的情况下，通过轮询测试密文1倒数第一位在0x43，且给倒数第二个随便一个数也都能通过的情况下，可以断定此时明文2就是0x01，于是我们就可以得到第二段明文2的的倒数第一位的中间值 Inermediary Value，由0x43 ^ 0x1 = 0x42现在可以控制它倒数第一位的明文了，啊真是太美妙辣！XD

然后我们就可以开始推他倒数第二位了，这里倒数第二位这个就要用到0x02来补padding规则了，倒数第一位变为0x02这个简单用我们获取到的0x42 ^ 0x2 = 0x40改一下密文1的倒数第一位，倒数第二位的话接着轮询到不报错即可，因为第一位这里保证是0x02所有不需要对第三位测了。

Ciphertext

1[0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0xe9 0x40]

2[0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00]

Plaintext

1[0x3d 0x10 0xc6 0xbc 0x68 0xe7 0xdd 0xc4 0xc1 0x75 0x65 0x85 0x6a 0x3d 0xe9 0x92]

2[0x4a 0xec 0xf6 0xed 0x58 0xfc 0xdc 0xa4 0xa3 0x4a 0x39 0x25 0x39 0x5b 0x02 0x02]

很好，这里我努力跑出了明文2倒数第二位在密文1倒数第二位为0xe9时他就不报错了（草），可以看到明文2倒数第二位就变成0x02，符合padding规则所以他就不报错了，于是我们就可以得知明文2的倒数第二个值的中间值 Inermediary Value为0xe9 ^ 0x02 = 0xeb，接下来就可以继续跑第三个值了。

Ciphertext

1[0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x58 0xe8 0x41]

2[0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00]

Plaintext

1[0x3d 0x10 0xc6 0xbc 0x68 0xe7 0xdd 0xc4 0xc1 0x75 0x65 0x85 0x6a 0x3d 0xe9 0x92]

2[0x4a 0xec 0xf6 0xed 0x58 0xfc 0xdc 0xa4 0xa3 0x4a 0x39 0x25 0x39 0x03 0x03 0x03]

这里有了倒数第一位的iv和倒数第二位的iv就可以直接异或0x03得出明文2他们对应0x3在密文1对应的位数上应该是啥值了，就不多赘述了，这里确保了明文2的倒数第二第三位是0x3之后就继续跑密文2的倒数第三位，直到不报错，就说明明文2倒数第三位也等于0x3满足padding的规则了就。

然后再用这里跑出来密文1倒数第三位的0x3d再异或一下0x3就得到了明文2倒数第三位的iv…依次往后类推就完事了

我写不动了，就是跑出来的就的改一下然后接着跑下一位，满足padding规则就不报错了，然后异或一下这一位补位的值就拿到了iv，再跑出来的都再改改，接着跑下一位。

Ciphertext

1[0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0x00 0xe8 0x00]

2[0xXX 0xXX 0xXX 0xXX 0xXX 0xXX 0xXX 0xXX 0xXX 0xXX 0xXX 0xXX 0xXX 0xXX 0xXX 0xXX] 这里懒就用XX代替一下这个block跑出来的iv异或出的要实现的值。

然后就可以计算上一个区块了，或者下一个区块..看自己喜欢吧，反正新block的第一个都是从0x01开始跑和上面一开始写的流程是一样.

Tags

Categories

Recent Posts

padding oracle attack 原理

上面的都沾点废话了，就是基础的补位，下面才是正经的部分

这里是padding oracle attack